After having analyzed in a previous post the problem of how to find out if, in an array of integers, there are two elements whose sum gives a value x, let’s now analyze and find the solution to another problem submitted directly to me during the second phone interview by Amazon for a Software Development Engineer position.
The problem this time is the following: given an array of integers where each element appears an even number of times and only one element appears an odd number of times, find the latter.
We will proceed step by step, analyzing three different solutions:
1) the brute force approach: for each element it counts its occurrences comparing it with all the other elements
2) a solution that consists in sorting the array and then comparing successive elements (the one I presented at the interview)
3) an improved version of solution 2), suggested to me by my interviewer.
Let’s consider solution 1)
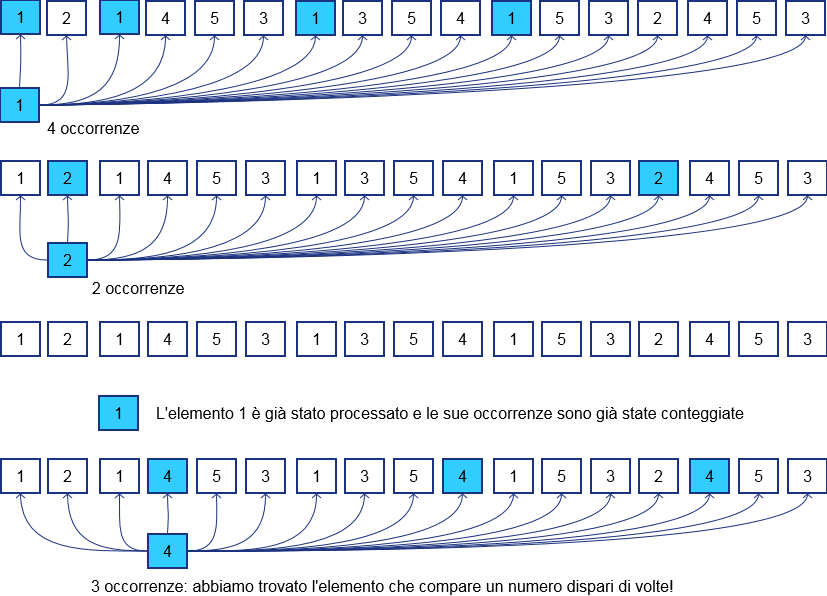
Take the first element and compare it with all the following, by counting the number of occurrences. Once the first iteration is completed, analyze the next and, if different from the previous, proceed in counting its occurrences within the array. Proceed in this way until all the elements occurrences have been counted, of course skip the elements already processed.
The image below shows an example of the result we obtain by running this algorithm:
Let’s move on to the implementation. First we have to decide what structure to use to maintain the list of items already processed. We can use a simple array and each time we start to iterate over a new item we previously check if this element is already present in the array.
In the following implementation we use instead an hash map, where we insert for each processed element also the number of its occurrences. Before analyzing each element we try to get it from the map to see if it already exists and, in that case, we just skip it.
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class AmazonFindOccOddTimes {
public static int findElementOddTimesBruteForce(int[] i){
Map done = new HashMap();
int c=0;
for(int x=0; x<=(i.length-1); x++) {
if (done.get(i[x]) == null) { // check if the element has already been processed
for(int y=0; y<=(i.length-1); y++) {
if (i[x] == i[y])
c++;
}
if ((c%2) != 0)
return i[x];
done.put(i[x], c); // insert the element in the map of processed elements
c = 0;
}
}
return -1; // suppose it's the return value for "value not found"
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
// In this case the element we are looking for is not present
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5};
int x = findElementOddTimesBruteForce(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBruteForce(input2);
System.out.println("Result: " + x);
}
}
The result we get by running the program is:
Result: 4 ------ Result: -1
As we saw through the graphical illustration, 4 is the element of the example array that appears an odd number of times.
This output, however, doesn't give us any indication about how the algorithm works, so we add some debug print to see what really happens. We change our method as follows:
public static int findElementOddTimesBruteForce(int[] i){
Map done = new HashMap();
int c=0;
for(int x=0; x<=(i.length-1); x++) {
if (done.get(i[x]) == null) {
for(int y=0; y<=(i.length-1); y++) {
if (i[x] == i[y])
c++;
}
System.out.println(i[x] + " occours " + c + " times");
if ((c%2) != 0)
return i[x];
done.put(i[x], c);
c = 0;
}
else { // get method finds the value inside the map
System.out.println("Element " + i[x] + " already processed.");
}
}
return -1; // suppose it's the return value for "value not found"
}
By running the program again this time we get in output something more meaningful:
1 occours 4 times 2 occours 2 times Element 1 already processed. 4 occours 3 times Result: 4 ------ 1 occours 4 times 2 occours 2 times Element 1 already processed. 4 occours 4 times 5 occours 4 times 3 occours 4 times Element 1 already processed. Element 3 already processed. Element 5 already processed. Element 4 already processed. Element 1 already processed. Element 5 already processed. Element 3 already processed. Element 2 already processed. Element 4 already processed. Element 4 already processed. Element 3 already processed. Element 5 already processed. Result: -1
Let us now analyze the algorithm complexity in terms of the number of elements comparisons performed according to the size N of the input. The general idea is that each element is compared with all the others in order to count the number of its occurrences; as we have seen, however, a value that has already been processed is skipped and its count is not repeated. We also need to consider the comparison performed to check if an item has already been processed or not. The latter is done once for each element, so N times.
The worst case is the one where each element appears 2 times (the minimum even number of times as possible) and the element that appears an odd number of times is the last of the array (or it does not exist ). In this case, half of the elements is compared with all the array elements. By adding also the operation to check if the item has already been processed, we get a result in terms of ((n/2) * n) + n that brings us to a quadratic complexity: O(n^2)
Let's consider solution 2)
We try to address the problem in a different way and see if we can reduce the complexity of the problem. This solution is the one I provided during the phone interview and consists of:
- To sort the array
- Compare two by two consecutive elements and keep a counter for the occurrences of the element
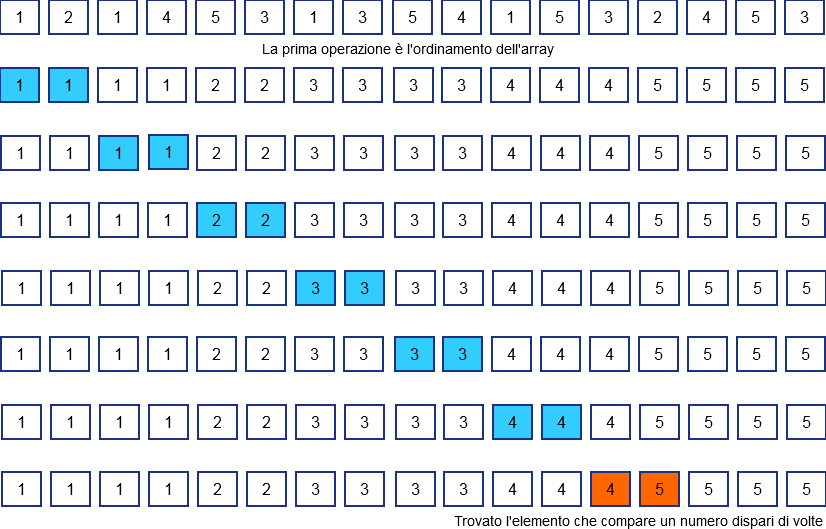
The image below shows the performance of this algorithm running on the sample array used before; as we can see, at first the array has been ordered and then elements are compared with each other and the counter of occurrences of the element under processing is updated. Whenever two elements differ we check the value of the counter and if it's odd we found our element, otherwise we reset the counter and proceed counting the occurrences of the new element.
Now that we have seen how this new solution works, we can move to its implementation.
import java.util.Arrays;
public class AmazonFindOccOddTimes {
public static int findElementOddTimes(int[] i){
Arrays.sort(i);
int c = 1;
int x, y;
for( x=0, y=1; y<=(i.length-1); x++, y++) {
if (i[x] == i[y]) {
c++;
if ((y==(i.length-1)) && ((c%2) != 0) )
return i[x];
}
else {
if ((c%2) != 0)
return i[x];
c = 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
// In this case the element we are looking for is not present
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5};
// In this case the element we are looking for is the last one after the array is sorted
int[] input3 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3};
int x = findElementOddTimes(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimes(input2);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimes(input3);
System.out.println("Result: " + x);
}
}
To test this solution we add a new test case, related to the case where the element we're looking for is the last one after we sort the array. This is in fact a particular case, useful to test both the behavior of the comparisons loop and of that the termination logic.
Executing the program we get the following output:
Result: 4 ------ Result: -1 ------ Result: 5
We add again some print on screen instruction to obtain detailed information on the various steps performed by the algorithm.
public static int findElementOddTimes(int[] i){
Arrays.sort(i);
int c = 1;
int totComp = 0;
int x, y;
for( x=0, y=1; y<=(i.length-1); x++, y++) {
totComp++;
if (i[x] == i[y]) {
c++;
if ((y==(i.length-1)) && ((c%2) != 0) ){
System.out.println(i[x] + " occours " + c + " times");
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
}
else {
System.out.println(i[x] + " occours " + c + " times");
if ((c%2) != 0) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
c = 1;
}
}
System.out.println(i[x] + " occours " + c + " times");
System.out.println("Number of comparisons: " + totComp);
return -1;
}
Re-running the program again we get the following result, where are highlighted the number of occurrences for each element and the final number of comparisons performed by the algorithm.
1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 3 times Number of comparisons: 13 Result: 4 ------ 1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 4 times 5 occours 4 times Number of comparisons: 17 Result: -1 ------ 1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 4 times 5 occours 3 times Number of comparisons: 16 Result: 5
In this case, the total algorithm complexity is given by the cost of the sorting algorithm + the number of comparisons performed to count the occurrences of each value that, in the worst case, is equal to (n-1). Assuming we use a sorting algorithm such as Quicksort with a complexity on average case of O (n * logn) the
execution cost of this solution is: n * logn + (n-1) , that is O(n * logn)
Let's consider solution 3)
The previous solution can be further improved, reducing the number of comparisons between the elements performed by the algorithm. Here we see how this new version works. I reached this solution during the phone interview, after my interviewer gave me a hint wondering, in relation to the previous solution are you sure that we actually need all these comparisons?
This question made me think and in fact I came to the conclusion that some of the comparisons executed by my solution were unnecessary. In fact, it is not necessary to compare the first element with the second one and then again the second element with the third one, updating the counter. To find the element that appears an odd number of times, in fact, is enough to compare the elements two by two, without repetition. We can compare the first and the second and, if they are equal, we proceed by comparing the third with the fourth, and so on. When there are two elements that are not equal, the first of the two in order of appearance in the array is the one that appears an odd number of times.
The image below shows the performance of this new improved solution on the usual example array used so far:
In this case we don't need a counter that counts the occurrences of each element but we know that, when we compare two elements that are different, the first of them appears an odd number of times.
We implement in Java this new optimized solution and we test on our 3 usual test cases; also with this solution, the test case where the last element resulting from the operation of sorting is the one that appears an odd number of times is particularly interesting.
import java.util.Arrays;
public class AmazonFindOccOddTimes {
public static int findElementOddTimesBetter(int[] i){
Arrays.sort(i);
int x, y;
for( x=0, y=1; y<=(i.length-1); x+=2, y+=2) {
if (!(i[x] == i[y])) {
return i[x];
}
}
if (x==(i.length-1))
return i[x];
return -1;
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
// In this case the element we are looking for is not present
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5};
// In this case the element we are looking for is the last one after the array is sorted
int[] input3 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3};
int x = findElementOddTimesBetter(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBetter(input2);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBetter(input3);
System.out.println("Result: " + x);
}
}
The result of the program execution is as follows:
Result: 4 ------ Result: -1 ------ Result: 5
Again, we print out some additional information as output. In particular, we show again the total number of elements comparisons performed by the algorithm, in order to see the difference with the previous solution.
public static int findElementOddTimesBetter(int[] i){
Arrays.sort(i);
int x, y;
int totComp = 0;
for( x=0, y=1; y<=(i.length-1); x+=2, y+=2) {
totComp++;
if (!(i[x] == i[y])) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
}
if (x==(i.length-1)) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
System.out.println("Number of comparisons: " + totComp);
return -1;
}
Number of comparisons: 7 Result: 4 ------ Number of comparisons: 9 Result: -1 ------ Number of comparisons: 8 Result: 5
As we can see the number of comparisons executed has been significantly reduced for each of the test cases, passing respectively:
from 13 to 7
from 17 to 9
from 16 to 8
As we said, the special case in which the last item is the one that appears an odd number of times is interesting and deserves to be analyzed separately. The following figure illustrates the steps executed by the procedure in this case:
The last element is not processed by the for loop, because after the previous iteration, the value of y "exceeds" the length of the array, and then it makes the condition false. The value x coincides instead with the position of the last element, and this shows us that this element is "unpaired" and so it is the element we're looking for.
The whole code of the 3 solutions and the examples can be downloaded here:



Very well explained. Thank you!
Thank you for your feedback
You can simply xor all the integers in the given array.
just simply `xor` all the elements in the given array of ints
int ans = input[0];
for (int i=1; i<input.length; i++) {
ans ^= input[i];
}
System.out.println("ans = "+ans);
Agree with Lee Wei.
The key to the question is ‘odd’ number of times and that there is only one element that appears an odd number of times. When you xor an element with itself the result is zero, so by xoring all the elements together, you are guaranteed to wind up with the resulting value to be the actual value of the odd-man-out element, as it were.
Done.
Partially agree, if the input is terabytes of data, do you even want to stream to the end (yes, no other choice)? The implementation proposed opt out soon as it discovers mismatch. XOR is nice on unsorted list because it’s streamed in due to large size which cannot fit in memory, while sorted is nice if fit in memory. In fact once sorted, there maybe ways to split it at boundaries and odd count list just needs to be searched…