Dopo aver analizzato in un post precedente il problema di come trovare se in un array di interi ci sono due elementi che sommati tra loro danno un valore x vediamo ora di analizzare e trovare la soluzione ad un altro problema che mi è stato sottoposto durante il secondo colloquio telefonico in Amazon per la posizione di Software Development Engineer.
Il problema questa volta è il seguente: dato un array di interi in cui ogni elemento compare un numero pari di volte ed un solo elemento compare un numero dispari di volte, trovare quest’ultimo.
Procederemo per gradi, analizzando 3 diverse soluzioni:
1) l’approccio forza bruta, che per ogni elemento conta le sue occorrenze confrontandolo con tutti gli altri elementi
2) una soluzione che prevede l’ordinamento dell’array e poi il confronto di elementi successivi (quella che ho presentato durante il colloquio)
3) una versione migliorata della soluzione 2), che mi è stata suggerita dal mio interlocutore durante il colloquio
Vediamo la soluzione 1)
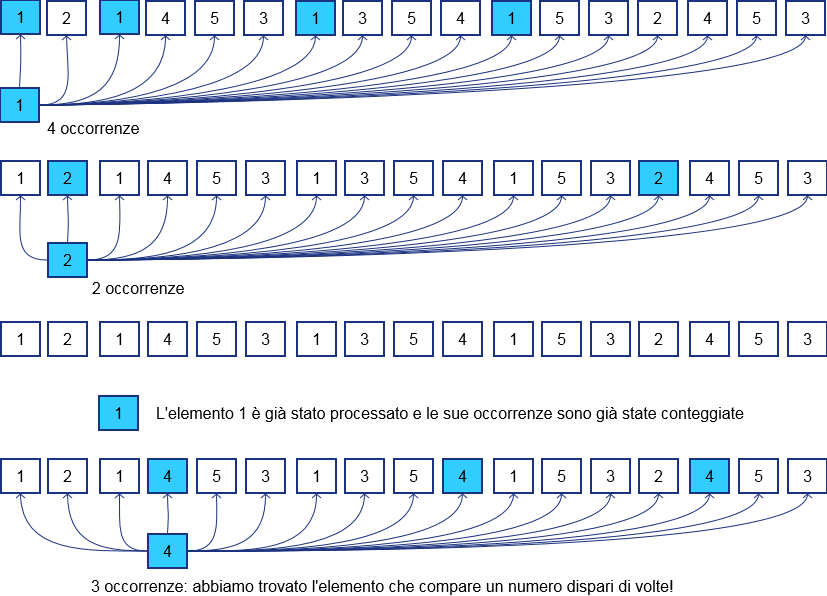
Il primo approccio consiste nel prendere il primo elemento e confrontarlo con tutti i seguenti, contando il numero delle sue occorrenze. Una volta terminata la prima iterazione si passa ad analizzare il successivo e, qualora non sia uguale al precedente, si procede con il conteggio delle sue occorrenze all’interno dell’array. Si procede in questo modo fino a quando non si sono conteggiate le occorrenze di tutti gli elementi, saltando ovviamente ogni volta gli elementi che sono già stati processati.
L’immagine seguente mostra un esempio di esecuzione di questo algoritmo:
Passiamo all’implementazione. Per prima cosa dobbiamo decidere in quale struttura mantenere la lista degli elementi già processati. Possiamo utilizzare un semplice array e, ogni volta che iniziamo ad iterare su un nuovo elemento, prima di farlo controlliamo se tale elemento è già presente in questo array.
Nell’implementazione seguente invece utilizziamo di una hash map, in cui inseriamo per ogni elemento processato anche il numero delle sue occorrenze. Prima di analizzare ogni elemento, si fa una get dell’elemento nella map per vedere se è già presente ed in tal caso lo si salta.
import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class AmazonFindOccOddTimes {
public static int findElementOddTimesBruteForce(int[] i){
Map done = new HashMap();
int c=0;
for(int x=0; x<=(i.length-1); x++) {
if (done.get(i[x]) == null) { // controllo se l'elemento e' gia' stato processato
for(int y=0; y<=(i.length-1); y++) {
if (i[x] == i[y])
c++;
}
if ((c%2) != 0)
return i[x];
done.put(i[x], c); // inserisco l'elemento tra quelli processati
c = 0;
}
}
return -1; // supponiamo sia il codice di ritorno per "valore non trovato"
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5}; // L'elemento da trovare non e' presente
int x = findElementOddTimesBruteForce(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBruteForce(input2);
System.out.println("Result: " + x);
}
}
Il risultato che otteniamo eseguendo il programma è:
Result: 4 ------ Result: -1
Come abbiamo visto tramite l'illustrazione grafica, 4 è l'elemento del nostro array di esempio che compare un numero dispari di volte.
Questo output però non ci da nessuna indicazione sul procedimento seguito dall'algoritmo, per cui aggiungiamo qualche stampa di debug per vedere cosa succede realmente. Modifichiamo il nostro metodo come segue:
public static int findElementOddTimesBruteForce(int[] i){
Map done = new HashMap();
int c=0;
for(int x=0; x<=(i.length-1); x++) {
if (done.get(i[x]) == null) {
for(int y=0; y<=(i.length-1); y++) {
if (i[x] == i[y])
c++;
}
System.out.println(i[x] + " occours " + c + " times");
if ((c%2) != 0)
return i[x];
done.put(i[x], c);
c = 0;
}
else { // la get nella map trova il valore
System.out.println("Element " + i[x] + " already processed.");
}
}
return -1; // supponiamo sia il codice di ritorno per "valore non trovato"
}
Eseguendo nuovamente il programma questa volta otteniamo come output qualcosa di più significativo:
1 occours 4 times 2 occours 2 times Element 1 already processed. 4 occours 3 times Result: 4 ------ 1 occours 4 times 2 occours 2 times Element 1 already processed. 4 occours 4 times 5 occours 4 times 3 occours 4 times Element 1 already processed. Element 3 already processed. Element 5 already processed. Element 4 already processed. Element 1 already processed. Element 5 already processed. Element 3 already processed. Element 2 already processed. Element 4 already processed. Element 4 already processed. Element 3 already processed. Element 5 already processed. Result: -1
Analizziamo adesso la complessità dell'algoritmo in termini del numero di confronti tra gli elementi che deve eseguire in base alla dimensione N dell'array di input. L'idea generale è che ogni elemento venga confrontato con tutti gli altri per contare il numero delle sue occorrenze; come abbiamo visto però, un valore che è già stato processato viene skippato ed il conteggio non viene ripetuto. Inoltre dobbiamo considerare anche il controllo effettuato per verificare se un elemento è già stato processato o meno. Quest'ultimo viene effettuato una volta per ciascun elemento, quindi N volte.
Il caso peggiore è quello in cui ciascun elemento compare 2 volte (il minimo numero pari di volte possibile) e l'elemento che compare un numero dispari di volte è l'ultimo dell'array (o non esiste). In questo caso, la metà degli elementi presenti viene confrontata con tutti gli elementi dell'array. Sommando anche l'operazione di verifica se l'elemento è già stato processato, otteniamo come risultato dell'analisi il valore ((n/2)*n) + n che ci porta ad una complessità quadratica: O(n^2)
Vediamo la soluzione 2)
Proviamo ad affrontare il problema in un altro modo e vediamo se riusciamo a ridurre la complessità dell'algoritmo di risoluzione del problema. Questa soluzione è quella che ho fornito durante il colloquio telefonico e che consiste in:
- effettuare l'ordinamento dell'array
- confrontare a due a due gli elementi consecutivi e tenere ogni volta un contatore delle occorrenze dell'elemento
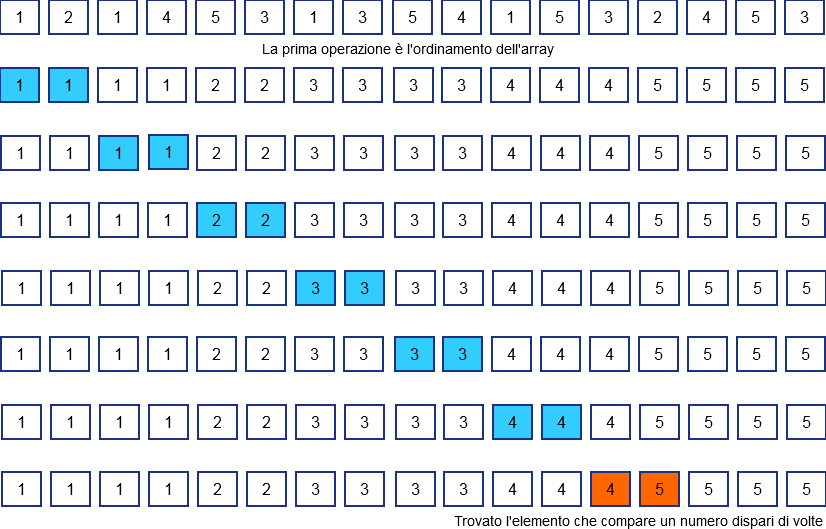
L'immagine seguente mostra l'esecuzione di questo algoritmo sull'array di esempio utilizzato precedentemente; come si può vedere l'array viene dapprima ordinato e poi gli elementi sono confrontati tra loro e viene aggiornato un contatore delle occorrenze dell'elemento che si sta analizzando. Ogni volta che i due elementi differiscono si controlla il valore del contatore e se è dispari abbiamo trovato l'elemento ricercato, altrimenti il contatore viene azzerato e si procede con il conteggio delle occorrenze del nuovo elemento.
Ora che abbiamo visto il procedimento su cui si basa questa nuova soluzione, passiamo alla sua implementazione.
import java.util.Arrays;
public class AmazonFindOccOddTimes {
public static int findElementOddTimes(int[] i){
Arrays.sort(i);
int c = 1;
int x, y;
for( x=0, y=1; y<=(i.length-1); x++, y++) {
if (i[x] == i[y]) {
c++;
if ((y==(i.length-1)) && ((c%2) != 0) )
return i[x];
}
else {
if ((c%2) != 0)
return i[x];
c = 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5}; // L'elemento da trovare non e' presente
int[] input3 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3}; // L'elemento da trovare e' l'ultimo dopo aver odrinato l'array
int x = findElementOddTimes(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimes(input2);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimes(input3);
System.out.println("Result: " + x);
}
}
Nel testing di questa soluzione aggiungiamo un nuovo test case, relativo al caso in cui l'elemento da trovare all'interno dell'array sia l'ultimo a seguito dell'operazione di ordinamento dell'array. Questo rappresenta infatti un caso particolare, per il quale testare il corretto funzionamento sia del ciclo dei confronti che della logica di terminazione del metodo.
Eseguendo il programma otteniamo l'output seguente:
Result: 4 ------ Result: -1 ------ Result: 5
Anche questa volta aggiungiamo qualche istruzione di stampa a video in modo da ottenere delle informazioni dettagliate sui vari passi eseguiti dall'algoritmo.
public static int findElementOddTimes(int[] i){
Arrays.sort(i);
int c = 1;
int totComp = 0;
int x, y;
for( x=0, y=1; y<=(i.length-1); x++, y++) {
totComp++;
if (i[x] == i[y]) {
c++;
if ((y==(i.length-1)) && ((c%2) != 0) ){
System.out.println(i[x] + " occours " + c + " times");
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
}
else {
System.out.println(i[x] + " occours " + c + " times");
if ((c%2) != 0) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
c = 1;
}
}
System.out.println(i[x] + " occours " + c + " times");
System.out.println("Number of comparisons: " + totComp);
return -1;
}
Rieseguendo nuovamente il programma otteniamo il risultato seguente, in cui viene evidenziato il numero di occorrenze per ciascun elemento ed il numero finale di confronti eseguiti dall'algoritmo.
1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 3 times Number of comparisons: 13 Result: 4 ------ 1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 4 times 5 occours 4 times Number of comparisons: 17 Result: -1 ------ 1 occours 4 times 2 occours 2 times 3 occours 4 times 4 occours 4 times 5 occours 3 times Number of comparisons: 16 Result: 5
In questo caso la complessità totale dell'algoritmo è data dal costo dell'algoritmo di ordinamento + il numero di confronti eseguiti per contare le occorrenze di ciascun valore che, nel caso peggiore, è uguale ad (n-1). Supponendo di utilizzare un algoritmo di ordinamento come il Quicksort che ha complessità nel caso medio pari a O(n*logn) il costo di
esecuzione di questa soluzione è: n*logn + (n-1), quindi O(n*logn)
Vediamo la soluzione 3)
La soluzione precedente può essere ulteriormente migliorata, riducendo il numero di confronti tra gli elementi che vengono effettuati dall'algoritmo. Di seguito vediamo come funzione questa nuova versione, alla quale sono giunto, durante il colloquio telefonico, dopo che il mio intervistatore mi ha dato un suggerimento domandandomi, in relazione alla soluzione precedente sei sicuro che servano proprio tutti quei confronti?
Questa domanda mi ha fatto riflettere ed in effetti, pensandoci, sono arrivato alla conclusioni che alcuni dei confronti che effettuava la mia soluzione erano superflui. Infatti, non è necessario confrontare il primo elemento con il secondo e poi nuovamente il secondo elemento con il terzo, aggiornando il contatore. Per trovare l'elemento che compare un numero dispari di volte, infatti, basta confrontare gli elementi due a due, senza ripetizioni. Si deve confrontare cioè il primo ed il secondo tra loro e, se sono uguali, si procede confrontando il terzo con il quarto e cosÏ via. Quando si trovano due elementi che non sono uguali, il primo dei due in ordine di apparizione nell'array è quello che compare un numero dispari di volte.
L'immagine seguente mostra l'esecuzione di questa nuova soluzione migliorata sul solito array di esempio usato finora:
In questo caso non ci serve tenere un contatore che conta le occorrenze di ciascun elemento ma sappiamo che, quando due elementi che confrontiamo sono diversi, è perchè il primo dei due compare un numero dispari di volte.
Implementiamo in codice Java questa nuova soluzione ottimizzata e la testiamo sui nostri 3 test case soliti; anche utilizzando questa soluzione, il test case che prevede che sia l'ultimo elemento risultante dall'operazione di ordinamento a comparire un numero dispari di volte risulta particolarmente interessante.
import java.util.Arrays;
public class AmazonFindOccOddTimes {
public static int findElementOddTimesBetter(int[] i){
Arrays.sort(i);
int x, y;
for( x=0, y=1; y<=(i.length-1); x+=2, y+=2) {
if (!(i[x] == i[y])) {
return i[x];
}
}
if (x==(i.length-1))
return i[x];
return -1;
}
public static void main(String[] args) {
int[] input = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 5, 3};
int[] input2 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3, 5}; // L'elemento da trovare non e' presente
int[] input3 = {1, 2, 1, 4, 5, 3, 1, 3, 5, 4, 1, 5, 3, 2, 4, 4, 3}; // L'elemento da trovare e' l'ultimo dopo aver odrinato l'array
int x = findElementOddTimesBetter(input);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBetter(input2);
System.out.println("Result: " + x);
System.out.println("------");
x = findElementOddTimesBetter(input3);
System.out.println("Result: " + x);
}
}
Il risultato dell'esecuzione del programma è il seguente:
Result: 4 ------ Result: -1 ------ Result: 5
Ancora una volta, aggiungiamo la stampa di qualche informazione aggiuntiva come output. Nel caso specifico, visualizziamo nuovamente il numero totale di confronti tra gli elementi eseguiti dall'algoritmo, in modo da poter fare un paragone con la soluzione precedente.
public static int findElementOddTimesBetter(int[] i){
Arrays.sort(i);
int x, y;
int totComp = 0;
for( x=0, y=1; y<=(i.length-1); x+=2, y+=2) {
totComp++;
if (!(i[x] == i[y])) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
}
if (x==(i.length-1)) {
System.out.println("Number of comparisons: " + totComp);
return i[x];
}
System.out.println("Number of comparisons: " + totComp);
return -1;
}
Number of comparisons: 7 Result: 4 ------ Number of comparisons: 9 Result: -1 ------ Number of comparisons: 8 Result: 5
Come possiamo vedere il numero dei confronti effettuati si è notevolmente ridotto per ciascuno dei test case, passando nei vari casi:
da 13 a 7
da 17 a 9
da 16 a 8
Come abbiamo detto, il caso particolare in cui l'ultimo elemento è quello che compare un numero dispari di volte è interessante e merita di essere analizzato a parte. La figura seguente illustra i passi della procedura in questo caso:
L'ultimo elemento non viene processato dal ciclo for, in quanto dopo la precedente iterazione, il valore di y "esce" dalla lunghezza dell'array e quindi rende falsa la condizione. Il valore x coincide invece con la posizione dell'ultimo elemento e questo ci indica che tale elemento è "spaiato" e quindi è l'elemento che stiamo cercando.
L'intero codice delle 3 soluzioni e degli esempi è scaricabile qui: